belajar matematika dan fisika: Trigonometri (I)

Pengukuran Sudut

Ukuran Sudut dalam Derajat
1° adalah besar sudut yang dihasilkan oleh perputaran 1/360 keliling lingkaran.
${1}^{0}=\frac{1}{360}\ putaran$
${1}^{0}=60'$
$1'=60$

Ukuran Sudut dalam Radian

$besar\ sudut\ POQ\ =\frac{panjang\ busur\ PQ}{r}radian\ = \frac{r}{r}radian=1\ radian$

Hubungan Ukuran Derajat dengan Ukuran Radian

Panjang Busur dan Luas Sektor

$sudut\ \alpha \ dalam\ derajat :$

$Panjang\ busur\ AB\ = \frac{\alpha }{360}\times 2\pi r$

$Luas\ sektor\ \left(juring \right)\ AOB\ = \frac{\alpha }{360}\times \pi {r}^{2}$

$sudut\ \alpha\ dalam\ radian :$

$panjang\ busur\ AB\ = \alpha r$

$Luas\ sektor\ \left(juring \right)\ AOB\ = \frac{1}{2}\alpha {r}^{2}$

Perbandingan Trigonometri Suatu Sudut Segitiga Siku - Siku

$\sin A=\sin \alpha =\frac{BC}{AB}=\frac{a}{c}$
$\cos A=\cos \alpha =\frac{AC}{AB}=\frac{b}{c}$
$\tan A=\tan \alpha =\frac{BC}{AC}=\frac{a}{b}$
$\cot A=\cot \alpha =\frac{AC}{BC}=\frac{b}{a}$
$\sec A=\sec \alpha =\frac{AB}{AC}=\frac{c}{b}$
$\csc A=\csc \alpha =\frac{AB}{BC}=\frac{c}{a}$

Identitas trigonometri yang lain :
$\csc \alpha =\frac{1}{\sin \alpha };\ \sec \alpha =\frac{1}{\cos \alpha };\ \cot \alpha =\frac{1}{\tan \alpha }$
$\tan \alpha =\frac{\sin \alpha }{\cos \alpha };\ \cot \alpha =\frac{\cos \alpha }{\sin \alpha }$

Nilai Perbandingan Trigonometri untuk Sudut - Sudut Istimewa

Pembagian Sudut dalam Trigonometri

Kuadran I biasanya disebut sudut lancip, sedangkan kuadran II disebut sudut tumpul.

Sudut - Sudut Berelasi

Rumus Umum Perbandingan Trigonometri Sudut - Sudut Berelasi

dengan k adalah bilangan bulat dan $\alpha$ adalah sudut positif atau negatif.

jika k genap maka perbandingan trigonometri itu tetap (tidak berubah)

$\sin \rightarrow \sin ;\ \cos \rightarrow \cos;\ \tan \rightarrow \tan;\ \sec \rightarrow \sec$

Jika k ganjil maka perbandingan trigonometri berubah menjadi perbandingan trigonometri yang bersesuaian dan sebaliknya

$\sin \rightarrow \cos ;\ \tan \rightarrow \cot ;\ \sec \rightarrow \csc ;\ \cos \rightarrow \sin ;\ \cot \rightarrow \tan ;\ \csc \rightarrow \sec$

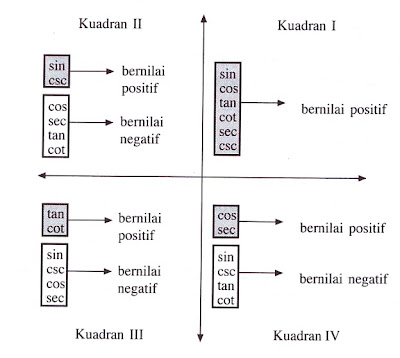
Nilai Perbandingan Trigonometri di Berbagai Kuadran

Perbandingan Trigonometri untuk Sudut $\color{blue}{\left(-\alpha \right)}$
$\sin \left(-\alpha \right)=-\sin \alpha$
$\cos \left(-\alpha \right)=\cos \alpha$
$\tan \left(-\alpha \right)=-\tan \alpha$
$\cot \left(-\alpha \right)=-\cot \alpha$
$\sec \left(-\alpha \right)=\sec \alpha$
$\csc \left(-\alpha \right)=-\csc \alpha$

Hubungan Koordinat Cartesius dan Koordinat Kutub

Jika diketahui koordinat kutub titik P adalah $\left(r,\ \alpha \right)$ maka koordinat Cartesius titik P adalah (x, y) yang ditentukan dengan hubungan :

$x=r\ \cos \alpha\ dan\ y=r\ \sin \alpha$

Jika diketahui koordinat Cartesius titik P adalah (x, y) maka koordinat kutub titik P adalah $\left(r,\ \alpha \right)$ yang ditentukan melalui hubungan :

$r=\sqrt{{x}^{2}+{y}^{2}}\ dan\ \tan \alpha =\frac{y}{x}$

Identitas Pyhtagoras
Untuk Setiap sudut x tertentu berlaku :

Persamaan Trigonometri Sederhana
Sudut dalam derajat :

Sudut dalam radian :

Nilai k persamaan di atas merupakan bilangan bulat..

Aturan Sinus

$Pada\ setiap\ \Delta ABC\ berlaku\ :\ \frac{a}{sin\ A}=\frac{b}{sin\ B}=\frac{c}{sin\ C}$
Aturan sinus dapat digunakan untuk mencari unsur - unsur segitiga yang belum diketahui, jika tiga unsurnya diketahui yaitu :

sisi - sudut - sudut
sudut - sisi - sudut
sisi - sisi - sudut

Aturan Cosinus

$Pada\ setiap\ \Delta ABC\ berlaku\ :$

Aturan cosinus dapat digunakan untuk mencari unsur - unsur segitiga yang unsur - unsurnya diketahui sebagai berikut :

sisi - sudut - sisi
sisi - sisi - sisi

Menentukan Besar Sudut suatu Segitiga
Jika semua sisi dalam segitiga diketahui maka besar sudut - sudut segitiga tersebut dapat ditentukan menggunakan aturan cosinus berikut :

Perlu diingat, sudut terbesar adalah sudut yang terletak di depan sisi terpanjang dan sudut terkecil adalah sudut yang menghadap sisi terpendek..

Menentukan Luas Segitiga dengan Besar Sudut dan Dua Sisi yang Mengapit Sudut itu Diketahui

$Pada\ setiap\ \Delta ABC\ berlaku\ :$

Menentukan Luas Segitiga dengan Besar Dua Sudut dan Satu Sisi yang Terletak di antara Kedua Sudut Diketahui
$Pada\ setiap\ \Delta ABC\ berlaku\ :$

Luas Segitiga dengan Ketiga Sisi Diketahui

Rumus Heran :
$L=\sqrt{s\left(s-a \right)\left(s-b \right)\left(s-c \right)}$
$s=\frac{1}{2}\left(a+b+c \right)$

Luas Segi-n Beraturan

Luas segi-n beraturan jika dinyatakan dengan L,maka :
$L=\frac{n }{2}\times {R}^{2}\times sin\frac{360^{\circ}}{n}$
Jika panjang sisi segi-n beraturan diketahui = p, dan luas segi-n beraturan itu dinyatakan dengan L, maka :
$L=\frac{n }{4}\times {p}^{2}\times \cot \frac{180^{\circ}}{n}$
Di bawah ini ada link untuk membantu siswa untuk memecahkan masalah trigonometri, sudut dinyatakan dalam radian :
Misal ada soal sebagai berikut :
Tentukan nilai x yang memenuhi persamaan sin (2x-30)= ½ dimana 0° ≤ x ≤ 360°...
Pembahasan :
Karena link diatas merupakan kalkulator online maka sudut harus dinyatakan dalam radian dulu ..
$\color{blue}{\sin \left(2x-\frac{\pi }{6} \right)=\sin \frac{\pi }{6}}$
$\color{blue}{\left(2x-\frac{\pi }{6} \right)=\frac{\pi }{6}+n.2\pi\ atau\ \left(2x-\frac{\pi }{6} \right)=\left(\pi -\frac{\pi }{6} \right)+n.2\pi }$
$\color{blue}{2x=\frac{\pi }{3}+n.2\pi \Rightarrow x=\frac{\pi }{6}+n.\pi }$
$\color{blue}{2x=\pi +n.2\pi \Rightarrow x=\frac{\pi }{2}+n.\pi }$
Karena n merupakan bilangan bulat maka kita bisa atur nilai n sedemikian rupa disesuaikan dengan interval jawabannya...
Ini link yang dimaksud :
My Trigonometry
Ingat link diatas hanya untuk mengecek jawaban kita, jadi langkah - langkah penyelesaian kita harus buat sendiri....!

Latihan Soal

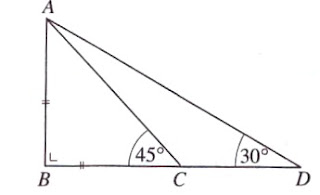
Perhatikan gambar di bawah ini. Apabila $AC=5\sqrt{2}$ maka panjang AD adalah...

Apabila $4.\cot x=3,\ dan\ 0^{\circ}<x<90^{\circ}$ maka nilai dari $\left(\frac{\sin x-\cos x}{\sin x+\cos x} \right)$ sama dengan...

$\color{red}{Jawab : \frac{1}{7}}$
Hitunglah nilai dari cos 2025°...

Jka diketahui tan 40° = a $\left(a\in R\ dan\ a\neq 0 \right)$ nyatakan bentuk berikut dalam a dari $\frac{\tan 140^{\circ}-\tan 130^{\circ}}{1+\tan 140^{\circ}.\tan 130^{\circ}}$

Buktikan identitas trigonometri berikut :

$\frac{\tan \alpha }{1-{\tan }^{2}\alpha }=\frac{\sin \alpha \cos \alpha }{{\cos }^{2}\alpha -{\sin }^{2}\alpha }$

Nilai dari :

Tentukan nilai dari :

$\frac{\sin 75^{\circ}.\cos 280^{\circ}.\tan 135^{\circ}}{\cos 345^{\circ}.\sin \ddot{190^{\circ}}.\cot 225^{\circ}}$

Jika $3.\sin \theta + 4.\cos \theta =5$ maka nilai dari $\sin \theta$ adalah....

Tentukan besar sudut jajargenjang jika dua sisi yang berdekatan dan diagonal persekutuan kedua sisi itu berturut - turut 5 cm, 10 cm, dan 11 cm..

Dalam segitiga ABC diketahui panjang sisi a = 2 kali panjang sisi c dan panjang sisi b = 1 ½ kali panjang sisi c. Hitunglah besar ∠A, ∠B, ∠C..

Dalam segitiga ABC, jika b² = a² + c² - ac, tunjukkan bahwa besar ∠B = 60°...

Dalam Δ ABC diketahui ∠A = 33°, panjang sisi a = 31,5 dan panjang sisi b = 51,8

Hitung besar ∠B (ada 2 kemungkinan)
Berilah penjelasan bahwa kedua ∠B yang diperoleh pada soal a) memenuhi

Dua perahu R dan S berjarak 10 km. Perahu S letaknya pada arah 110° dari R dan perahu T 170° dari R. Perahu T letaknya pada arah 210° dari S. Hitunglah jarak perahu T dari perahu R dan dari perahu S..

Dalam Δ ABC, panjang sisi a sama dengan 7 cm lebih panjang dari ½ panjang sisi b dan panjang sisi c sama dengan 1 cm lebih pendek dari 1¼ panjang sisi a. Keliling Δ ABC itu sama dengan 36 cm.

Hitunglah panjang sisi a, sisi b, dan sisi c
Hitunglah luas Δ ABC...

Dua kapal berlayar dari suatu pelabuhan pada saat bersamaan. Kapal A berlayar dengan arah 050° dan kecepatan layar 10 km/jam, sedangkan kapal B berlayar dengan arah 090° dan kecepatan layar 13 km/jam. Tentukan jarak antar kapal itu setelah berlayar selama 3 jam..

Pada Δ ABC diketahui ∠B = 30° dan ∠C = 120°. Jika a + b + c = 4 cm, hitunglah :

panjang sisi a
panjang sisi b
panjang sisi c

Sebuah kapal sedang berlabuh dalam posisi menghadap ke menara. Seorang pengamat (berada di puncak menara) melihat ujung depan kapal dengan sudut deviasi 75° (perhatikan gambar). jika tinggi pengamat 1,6 m, tinggi menara 75 m, dan dasar menara berada 15 m di atas permukaan laut, berapakah panjang kapal itu?

Adi dengan tinggi 1,60 m melihat puncak pohon dengan sudut elevasi 60°. Budi dengan tinggi 1,60 m melihat puncak pohon dengan sudut elevasi 75°. Jarak kedua orang itu adalah 6 m. Tentukan tinggi pohon itu..

Diberikan ΔABC dengan sudut - sudut α, β, γ. Jika luas ABC = 12√3 cm², a = 6 cm, dan b = 8 cm, hitunglah besar sudut γ...

Diberikan segi empat ABCD dengan AB = 20 cm, AD = 48 cm, CD = 14 cm, ∠ADC = 90°, dan ∠BAC = 30°. hitunglah luas segi empat ABCD..

Find all the angles, between 0 ° and 360°, which satisfy the equation :

16 sin x - 8 sin² x = 5 cos² x
4 sin y.cos y - 3 cos²y = 0
sec (3z/2 - 18°) + 2 = 0

Dari titik P, Ali mengamati puncak sebuah antena dengan sudut elevasi 45°. Kemudian Ali berjalan sejauh 12 meter mendekati kaki antena sampai di titik Q. Dari titik Q ini, Ali mengamati puncak antena dengan sudut elevasi 60°. Berapa meterkah tinggi antena itu?

seorang anak berdiri di samping tiang bendera. Tinggi anak itu 148 cm dan panjang bayangannya 120 cm. Jika panjang bayangan tiang bendera itu sama dengan 6 meter, berapa meterkah tinggi tiang bendera itu ?

Pesawat udara terbang dari landasan dengan arah 040° sejauh 300 km, kemudian dengan arah 310° sejauh 251,73 km, danakhirnya kembali ke landasan.

berapa panjang lintasan pada penerbangan yang terakhir ?
Tentukan arah penerbangan yang terakhir terhadap titik asal landasan

Pada segitiga ABC , diketahui panjang sisi AB = 7 cm, BC = 9 cm, dan AC = 8 cm. Nilai sin sisi terpanjang adalah...

Pada gambar di bawah, segitiga PQR lancip dan titik S adalah tengah - tangah QR atau QS = SR ( garis PS biasa disebut garis berat segitiga)

(PS)² = ½q² + ½r² - ¼p²
(PS)² = ¼q² + ¼r² + ½qr cos P

Sebidang tanah berbentuk segiempat. Titik - titik sudut tanah itu ditandai dengan tonggak - tonggak P, Q, R, dan S. Jarak tonggak P ke Q = 4 m, Q ke R = 3 m, R ke S = 6 m, P ke S = 4 m, dan Q ke S = 5 m. Hitunglah luas tanah itu....

Diketahui luas suatu segitiga sama kaki 8 cm², panjang kedua sisi yang sama 4,2 cm. Tentukan panjang sisi ketiga sama kaki itu..

Sebuah segienam beraturan memiliki keliling 72 cm. Luas segienam tersebut adalah....cm²
Diketahui x memenuhi persamaan 2 sin² x - 7 sin x + 3 = 0 untuk 0 ≤ x ≤ ½π. Nilai tan x =....
Perhatikan gambar berikut:

Diketahui segitiga ABC dengan panjang AB = 8 cm dan besar ∠ ABC = 60°. Jika luas Δ ABC = 24√3 cm², panjang sisi AC = ....cm
Puncak pohon terlihat oleh pengamat A dengan sudut elevasi 60° dan pengamat B dengan sudut elevasi 30°. Tinggi kedua pengamat adalah 1,6 m dan dengan jarak 15 m. Tentukan tinggi pohon..
Pada ΔABC , diketahui cos (B+C) = 9/40. Jika panjang sisi AC = 10 cm, AB = 8 cm, panjang sisi BC =...cm
Balon udara terlihat oleh pengamat A dengan sudut elevasi 60° dan pengamat B dengan sudut elevasi 45°. Jarak AB = 240 m. Hitunglah tinggi balon..

belajar matematika dan fisika

Laman

Minggu, 06 Januari 2013

Trigonometri (I)

10 komentar: