belajar matematika dan fisika: Kinematika dengan Analisis Vektor

Vektor Posisi
Posisi benda pada waktu tertentu pada gerak satu dimensi (gerak lurus) dinyatakan oleh x = x(t) atau y = y(t).
Sedangkan posisi partikel untuk gerak benda pada suatu bidang dinyatakan dengan vektor - vektor satuan dan dinyatakan oleh kedua persamaan di atas... r = x i + y j
Perpindahan
Perpindahan didefinisikan sebagai perubahan posisi suatu benda pada waktu tertentu. Perpindahan termasuk besaran vektor. Misal sebuah benda pada saat t₁, vektor posisinya r₁, dan pada saat t₂, vektor posisinya r₂, maka perpindahan partikel :
${\color{Blue} \Delta r=r_{2}-r_{1}=\left ( x_{2}i + y_{2}j \right )-\left ( x_{1}i + y_{1}j \right )}$
${\color{Blue} \Delta r=\Delta x\ i+\Delta y\ j}$
${\color{Blue} \Delta r=\sqrt{\left ( \Delta x \right )^{2}+\left ( \Delta y \right )^{2}}}$
${\color{Blue} Arah\ \Rightarrow \tan \theta =\frac{\Delta y}{\Delta x}}$
Kecepatan rata - rata
Merupakan hasil bagi perpindahan dengan selang waktu yang diperlukan..
Untuk gerak satu dimensi :
${\color{Blue} \bar{v}=\frac{\Delta s}{\Delta t}=\frac{\Delta x}{\Delta t}=\frac{\Delta y}{\Delta t}}$
Untuk gerak dua dimensi :
${\color{Blue} \bar{v}=\frac{\Delta r}{\Delta t}=\frac{r_{2}-r_{1}}{t_{2}-t_{1}}}$
${\color{Blue} \bar{v}=\bar{v_{x}}\ i+\bar{v_{y}}\ j}$
Kecepatan sesaat
Kecepatan benda pada saat tertentu..
Untuk gerak satu dimensi :
${\color{Blue} v=\frac{ds}{dt}=\frac{dx}{dt}=\frac{dy}{dt}}$
Untuk gerak dua dimensi :
${\color{Blue} v=\frac{dr}{dt}=v_{x}\ i + v_{y}\ j}$
Ketinggian maksimum
Ketinggian maksimum, y_maks dicapai jika dipenuhi syarat :
${\color{Blue} \frac{dy}{dt}=0\ atau\ v_{y}=0}$
Dari persamaan diatas akan diperoleh nilai t, setelah itu nilai t kita masukkan ke dalam persamaan komponen perpindahan vertikal y = y(t)
Menentukan posisi dari fungsi kecepatan
Untuk gerak satu dimensi :
${\color{Blue} s=s_{0}+\int v\ dt}$
${\color{Blue} s_{0}= posisi\ awal\ partikel}$
${\color{Blue} v=v(t)}$
Untuk gerak dua dimensi :
${\color{Blue} r=r_{0}+\int v\ dt}$
${\color{Blue} r_{0}=x_{0}\ i + y_{0}\ j= posisi\ awal\ partikel}$
${\color{Blue} v=v(t)=v_{0}\ i+v_{0}\ j}$
Percepatan rata - rata
Merupakan hasil bagi perubahan kecepatan Δv dengan selang waktunya..
Untuk gerak satu dimensi :
${\color{Blue} a=\frac{\Delta v}{\Delta t}}$
Untuk gerak dua dimensi :
${\color{Blue} a=\frac{\Delta v}{\Delta t}=\frac{v_{2}-v_{1}}{t_{2}-t_{1}}=\bar{a_{x}}\ i+\bar{a_{y}}\ j}$
Percepatan sesaat
Merupakan percepatan eksak suatu partikel pada saat tertentu..
Untuk gerak satu dimensi :
${\color{Blue} a=\frac{dv}{dt}}$
${\color{Blue} a=\frac{d^{2}s}{dt^{2}}=\frac{d^{2}y}{dt^{2}}=\frac{d^{2}x}{dt^{2}}}$
Untuk gerak dua dimensi :
${\color{Blue} a=\frac{dv}{dt}=\frac{d^{2}r}{dt^{2}}=a_{x}\ i + a_{y}\ j}$
Menentukan kecepatan dari fungsi percepatan
Untuk gerak satu dimensi :
${\color{Blue} v=v_{0}+\int a\ dt}$
${\color{Blue} v_{0}=kecepatan\ awal\ partikel}$
Untuk gerak dua dimensi :
${\color{Blue} v=v_{0}+\int a\ dt=v_{x}\ i+v_{y}\ j}$
${\color{Blue} v_{0}=v_{ox}\ i + v_{oy}\ j}$
Perpindahan dan jarak sebagai luas di bawah grafik v - t

Perpindahan dan jarak sebagai luas di bawah grafik v - t

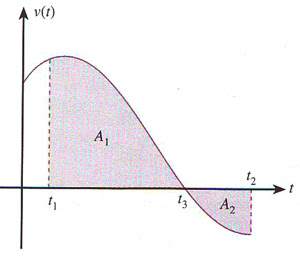
Dari gambar di atas kita dapat menentukan perpindahan dan jarak mulai dari t = t₁ samapai dengan t = t₂
${\color{Blue} Perpindahan = A_{1}-A_{2}=\int_{t_{1}}^{t_{2}}v(t)\ dt}$
${\color{Blue} Jarak = A_{1}+A_{2}=\int_{t_{1}}^{t_{3}}v(t)\ dt-\int_{t_{3}}^{t_{2}}v(t)\ dt}$
Yang perlu diingat :
Menghitung perpindahan dalam selang waktu t₁ ≤ t ≤ t₂ secara langsung dari fungsi integral tidak masalah. Tapi saat menghitung jarak dalam selang waktu t₁ ≤ t ≤ t₂, kita harus mengecek dulu apakah grafik itu memotong sumbu t atau tidak...
Kecepatan sesaat sebagai kemiringan grafik

Kecepatan sesaat pada t = t₁ adalah kemiringan garis singgung dari grafik posisi x - t pada saat t = t₁
${\color{Blue}v = tan\ \alpha =\frac{\Delta x}{\Delta t} }$
Percepatan sesaat sebagai kemiringan grafik v - t

Percepatan sesaat pada t = t₁ adalah kemiringan garis singgung dari grafik v - t pada t = t₁
${\color{Blue} a=\tan \alpha =\frac{\Delta v}{\Delta t}}$
Kecepatan sudut rata - rata
Merupakan hasil bagi perpindahan sudut (Δθ) dengan selang waktu tempuhnya (Δt)..
${\color{Blue} \bar{\omega } =\frac{\Delta \theta }{\Delta t}=\frac{\theta _{2}-\theta _{1}}{t_{2}-t_{1}}}$
Kecepatan sudut sesaat
Turunan pertama fungsi posisi sudut θ terhadap waktu :
${\color{Blue} \omega =\frac{d\theta }{dt}}$
Menentukan besar kecepatan sudut sesaat dari kemiringan grafik θ - t

Pada grafik di atas, kecepatan sudut sama dengan kemiringan grafik...
${\color{Blue} \omega =\tan \beta }$
Menentukan posisi sudut dari fungsi kecepatan sudut
${\color{Blue} \omega (t)=\frac{d\theta }{dt}\Rightarrow d\theta =\omega (t)dt\Rightarrow \int_{\theta _{0}}^{\theta }d\theta =\int_{0}^{t}\omega (t)dt}$
${\color{Blue} \theta -\theta _{0}=\int_{0}^{t}\omega (t)dt\Rightarrow \theta =\theta _{0}+\int_{0}^{t}\omega (t)dt}$
${\color{Blue} \theta _{0}=posisi\ sudut\ awal\ (rad)}$
Menentukan besar percepatan sudut dari kemiringan grafik ω - t

Pada grafik di atas, percepatan sudut sama dengan kemiringan grafik..
${\color{Blue} \alpha =\tan \beta }$
Percepatan sudut sebagai turunan dari fungsi kecepatan sudut
${\color{Blue} \alpha =\frac{d\omega }{dt}=\frac{d^{2}\theta }{dt^{2}}}$
Kecepatan sudut dari percepatan sudut
${\color{Blue} \alpha (t)=\frac{d\omega }{dt}\Rightarrow d\omega =\alpha (t)dt\Rightarrow \int_{\omega _{0}}^{\omega }d\omega =\int_{0}^{t}\alpha (t)\ dt}$
${\color{Blue} \omega -\omega _{0}=\int_{0}^{t}\alpha (t)\ dt\Rightarrow \omega =\omega _{0}+\int_{0}^{t}\alpha (t)\ dt}$
Kalau mau lihat latihan soal dan pembahasannya KSJA XI

belajar matematika dan fisika

Laman

Kamis, 06 Juni 2013

Kinematika dengan Analisis Vektor

2 komentar: